💠 Graphes

Sommaire

Exemples introductifs
Définitions
Vocabulaire sur les graphes non orientés
Vocabulaire sur les graphes orientés
- Variantes de vocabulaire
Représentation en Python
Parcours de graphe

Exemples introductifs

Réseaux et cartes

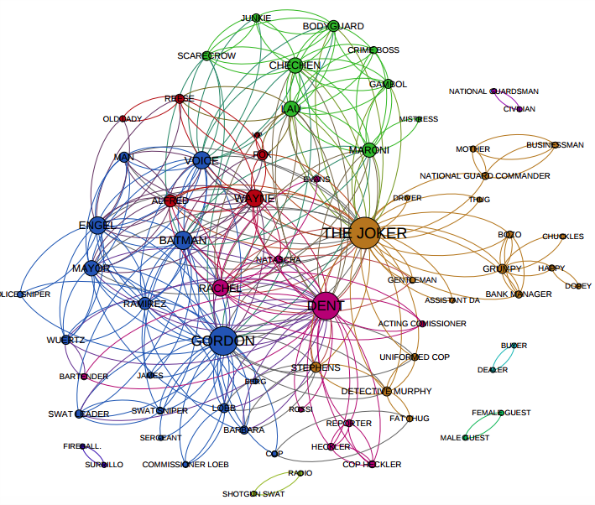
Sur ce graphe, on constate qu'il y a une grosse composante connexe, et quelques petites.

Réseau routier, cartes

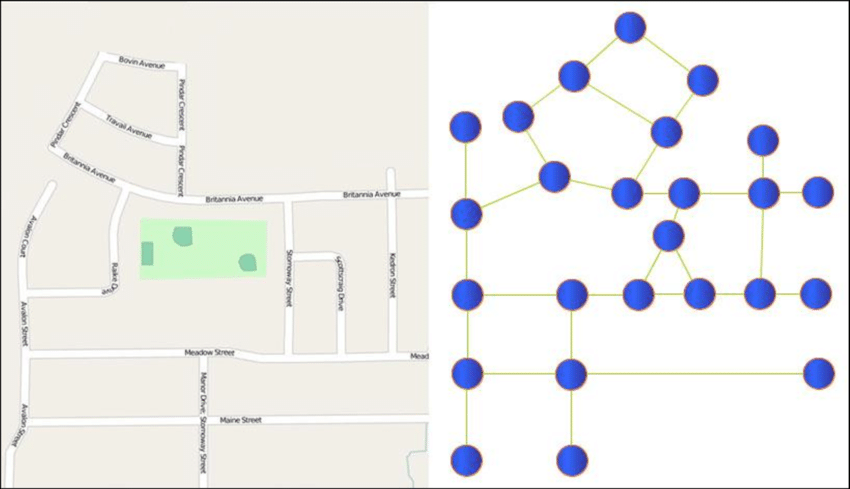
Sur ce graphe, les sommets sont des lieux sur la carte, et les arcs sont des routes les reliant.

On pourrait ajouter des flèches, pour indiquer les sens uniques. Dans ce cas, le graphe serait orienté.

Labyrinthe

Voici un labyrinthe qui n'est pas parfait, il y a un îlot. On ne peut pas en sortir en utilisant la technique de la main gauche (ou droite) si on part d'un point entre $D$ et $F$ .

À droite, on voit une modélisation sous forme de graphe, dont on pourra faire des parcours de graphe (en largeur ou en profondeur) pour résoudre des problèmes.

Positions à un jeu

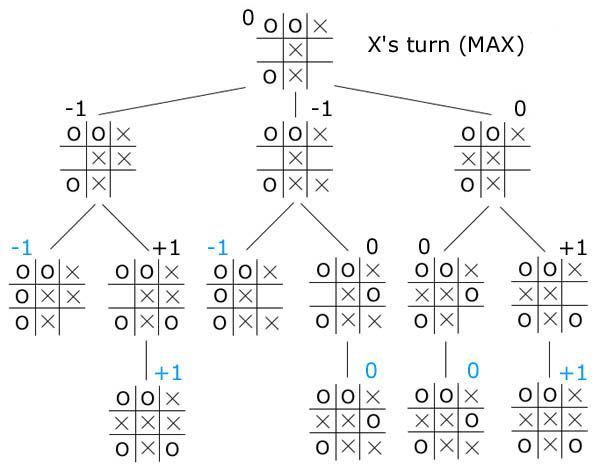
Dans un jeu où on ne retrouve pas deux fois dans la même partie la même position, le graphe des positions est sans cycle, donc un arbre. Ici, on peut prouver qu'il y a match nul pour deux joueurs qui ont la meilleure stratégie.

Les feuilles sont des parties finies, $-1$ pour une défaite de X, $+1$ pour une victoire, et $0$ pour un nul.
À chaque étage, pour remonter
- si c'est le tour de X, on prend le maximum des possibilités.
- Si c'est le tour de O, on prend le minimum des possibilités.

Graphes de prérequis

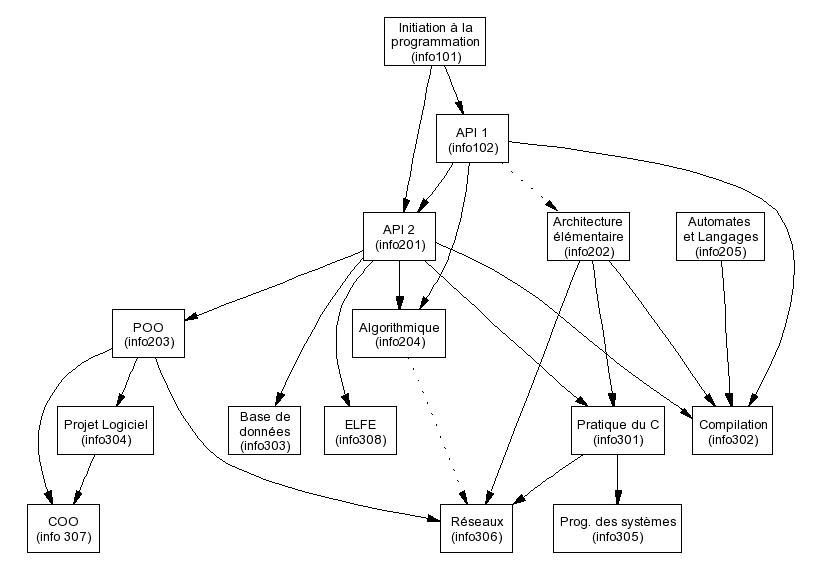
Ce graphe indique les modules requis pour accéder à d'autres dans un cursus universitaire en informatique, ou bien les lectures conseillées de chapitres avant d'aborder d'autres.

Graphes de dépendances

Ce genre de graphe est utilisé, par exemple, en compilation, où un source ne peut être compilé que si ses dépendances sont satisfaites... Il faut évidemment vérifier l'absence de cycle !

Définitions

Un graphe est un ensemble fini de sommets reliés entre eux par des arcs. On note souvent $G = (V, E)$ .

$V$ (pour Vertex, 'sommet' en anglais) est un ensemble fini ; ce sont les points ou sommets ou nœuds du graphe.
$E$ (pour Edge, 'arête' en anglais) est un ensemble fini de paires de sommets distincts qui définissent les arcs.
L'ordre d'un graphe est son nombre de sommets.
La taille d'un graphe est son nombre d'arcs.
Un graphe peut être orienté, les arcs ont chacun un sens.

Un graphe peut être non orienté, les arcs n'ont alors pas de sens en particulier. Dans ce cas on parle parfois d'arêtes.

Vocabulaire sur les graphes non orientés

Une chaîne est un ensemble fini non vide de sommets reliés deux à deux consécutivement par des arêtes distinctes.

Dans l'exemple précédent, [sommet_1, sommet_3, sommet_2] constitue une chaîne.

Un graphe non orienté est dit connexe si, pour toute paire de sommets, il existe une chaîne les reliant. Cela signifie que le graphe est en un seul morceau.

Par exemple, s'il n'y a pas de pont entre deux îles, le réseau routier de ces îles n'est pas connexe.

Si une chaîne relie un sommet à lui-même, on parle de cycle.

Dans l'exemple précédent, [sommet_1, sommet_3, sommet_4, sommet_1] constitue un cycle.

On a déjà évoqué qu'un arbre enraciné est un graphe non vide, connexe et sans cycle, avec un sommet particulier désigné comme racine.

Vocabulaire sur les graphes orientés

Un chemin est un ensemble fini de sommets reliés deux à deux consécutivement par des arcs.

Un graphe orienté est dit connexe, si sa version non orientée est connexe.

Un graphe orienté est dit fortement connexe, si, pour chaque paire de sommets, il existe un chemin les reliant.

L'exemple précédent est connexe, mais pas fortement connexe ; en effet il n'y a pas de chemin reliant $\text{D}$ à $\text{A}$ .

Nous verrons bientôt des algorithmes pour déterminer s'il existe un chemin d'un sommet à un autre, et pour déterminer la longueur du plus petit.

Si les arcs sont pondérés, on peut aussi s'intéresser au chemin entre deux sommets dont le coût total des arcs est le plus petit.

Variantes de vocabulaire

Parfois les sommets sont appelés nœuds.
Parfois les chemins sont définis par une liste d'arêtes ; c'est utile si le graphe n'est pas simple, et où plusieurs arcs relient la même paire de sommet.
Parfois, on autorise les boucles : un arc qui part d'un sommet pour arriver au même sommet. Ce ne sont plus des graphes simples ; on ne les voit pas en NSI, ils sont utilisés pour les automates en post BAC.

Représentation en Python

Il est très commode de faire une numérotation des sommets à partir de $0$ , et ainsi de disposer d'un tableau de sommets dont la longueur est l'ordre du graphe.

Matrice d'adjacence

Pour un graphe $G$ , pour chaque indice $0 \leqslant i < \text{ordre}(G)$ , on peut disposer d'un tableau encore de même longueur indiquant s'il y a un arc reliant le sommet $i$ aux sommets $j$ .

Par exemple, pour $G_1$ , on a :

adjacence[0] = [False, True, False, True]
adjacence[1] = [False, False, True, False]

Exercice 1. Compléter le code suivant :

adjacence = [
    [False, True, False, True],
    [False, False, True, False],
    ...
]
# adjacence est un tableau de tableaux de booléens

Que vaut adjacence[0][1] ? Et de manière générale, que signifie adjacence[i][j] ? Est-ce conforme à la pratique commune de désigner les lignes par leur indice $i$ et les colonnes par leur indice $j$ ?

On dit aussi que adjacence est une matrice de booléens. Et si on code True par $1$ et False par $0$ , on peut l'écrire aussi :

$\begin{pmatrix} 0 & 1 & 0 & 1 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ \end{pmatrix}$

Exercice 2. Dessiner le graphe dont la matrice d'adjacence est :

$\begin{pmatrix} 0 & 1 & 0 & 1 \\ 1 & 0 & 1 & 1 \\ 1 & 0 & 0 & 0 \\ 1 & 1 & 1 & 0 \\ \end{pmatrix}$

Exercice 3. Relire le cours et trouver la raison pour laquelle la diagonale principale ne comporte que des $0$ .

Implémentation Python

class Graphe:
    """Un graphe est ici représenté en interne par une matrice d'adjacence
       entre les sommets qui sont les entiers de 0 inclus à n exclu.
    n est l'ordre du graphe.
    """

    def __init__(self, n):
        self.n = n
        self.adjacence = [[False for j in range(n)] for i in range(n)]
    
    def ajout_arc(self, i, j):
        self.adjacence[i][j] = True
    
    def est_arc(self, i, j):
        return self.adjacence[i][j]
    
    def voisins(self, i):
        sommets_voisins_i = []
        for j in range(self.n):
            if self.adjacence[i][j]:
                sommets_voisins_i.append(j)
        return sommets_voisins_i

Le graphe précédent peut alors être construit avec le code :

g = Graphe(4)
g.ajout_arc(0, 1)
g.ajout_arc(0, 3)
g.ajout_arc(1, 2)
g.ajout_arc(3, 1)

Cette implémentation est certes simple, mais elle a des défauts. On note $n$ l'ordre d'un graphe $G$ , et $t$ sa taille (le nombre d'arcs).

On rappelle que :

$\mathcal O(1)$ signifie un coût constant.

$\mathcal O(n)$ signifie un coût proportionnel à $n$ uniquement.

$\mathcal O(n^2)$ signifie un coût proportionnel à $n^2$ uniquement.

$\mathcal O(n×t)$ signifie un coût proportionnel à $n$ et $t$ uniquement.

Exercice 4.

Quelle quantité de mémoire est utilisée ? $\mathcal O(1)$ ou $\mathcal O(n)$ ou $\mathcal O(n^2)$ ou $\mathcal O(n×t)$ ou autre ? Justifier.
Pour itérer sur les voisins de $i$ , quelle est la complexité ? $\mathcal O(n)$ ou $\mathcal O(n^2)$ ou $\mathcal O(n×t)$ ou autre ? Justifier.
Pour un graphe ayant un nombre de sommets très important, mais peu d'arcs (on parle de graphe peu dense), cette implémentation est-elle efficace ? Et pour un graphe dense ? Comment définiriez-vous un graphe dense ?

Dictionnaire d'adjacence

class Graphe:
    """Un graphe est ici représenté en interne par un dictionnaire d'adjacence
       entre des sommets qui sont toute étiquette possible.
    """

    def __init__(self):
        self.adjacence = dict() # un dictionnaire vide
    
    def ajout_sommet(self, sommet):
        if sommet not in self.adjacence:
            self.adjacence[sommet] = set() # un ensemble vide

    def ajout_arc(self, sommet_1, sommet_2):
        self.ajout_sommet(sommet_1)
        self.ajout_sommet(sommet_2)
        self.adjacence[sommet_1].add(sommet_2)
    
    def est_arc(self, sommet_1, sommet_2):
        if sommet_1 not in self.adjacence:
            raise KeyError(f"Le sommet_1 {sommet_1} n'existe pas")
        elif sommet_2 not in self.adjacence:
            raise KeyError(f"Le sommet_2 {sommet_2} n'existe pas")
        else:
            return sommet_2 in self.adjacence[sommet_1]
    
    def sommets(self):
        return list(self.adjacence)
    
    def voisins(self, sommet):
        if sommet not in self.adjacence:
            raise KeyError("Le sommet n'existe pas")
        else:
            return self.adjacence[sommet] # un ensemble

Exercice 5. Reprendre l'exercice 4, avec cette nouvelle implémentation.

Listes d'adjacences

Il est possible aussi d'utiliser des listes, en vérifiant bien l'absence de doublon.

Pour implémenter cette solution, on utilise souvent le principe de marquage des sommets, lorsqu'ils sont visités par exemple.

Sur un schéma, on leur met une couleur, ou on l'entoure.
Dans un programme, on modifie la valeur du sommet, par un code indiquant qu'il est visité. On peut même indiquer des informations plus pertinentes comme la distance minimale par rapport à un point de départ...

Parcours de graphe

Exercice 1

Reprendre le cours sur les ABR et le code pour le parcours en largeur, celui avec l'utilisation d'une file.
Remplacer la structure File par la structure Pile. Qu'obtient-on comme parcours ?
En déduire une façon de procéder aux parcours en largeur et en profondeur des graphes.
Votre méthode fonctionne-t-elle si le graphe contient un cycle ?

Exercice 2

Écrire une méthode donne_cycle(self, sommet) qui renvoie None si sommet ne fait partie d'aucun cycle, et sinon renvoie une liste de sommets, de sommet à sommet constituant un cycle.
En imaginant que vous travaillez avec un langage qui ne propose pas None et qui impose de renvoyer un résultat de même type pour chaque fonction, quelle solution de codage envisager dans le cas présent pour signifier l'absence de cycle.
Hors programme, mais facile. Même question que 2., en supposant la présence de boucle dans le graphe.

Exercice 3

Écrire une méthode sortie_courte(self, sommet) qui renvoie un plus court chemin de sommet vers un sommet sans successeur.

Exercice 4

Écrire une méthode chemin_court(self, initial, fin) qui renvoie un plus court chemin d'un sommet initial vers un sommet fin, et None s'il n'y en a pas.